Task 2
Question
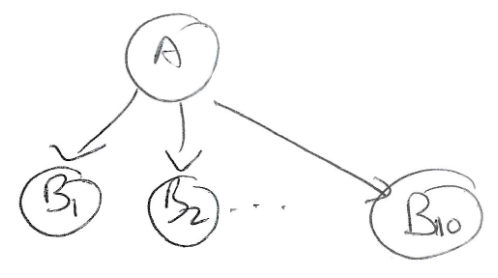
In a certain probability problem, we have 11 variables: A,
- Variable A has 7 values.
- Each of variables
, ..., have 8 possible values. Each is conditionally indepedent of all other 9 variables (with j != i) given A.
Based on these facts:
Part a
How many numbers do you need to store in the joint distribution table of these 11 variables?
Part b:
What is the most space-efficient way (in terms of how many numbers you need to store) representation for the joint probability distribution of these 11 variables? How many numbers do you need to store in your solution? Your answer should work with any variables satisfying the assumptions stated above.
Part c:
Does this scenario follow the Naive-Bayes model?
Answer
Part a
A 11 dimensional table 7 across one dimensions and 8 across the other dimension.
7,516,192,768 values in theory
(or)
7,516,192,767 in practice
Part b
Using Conditional Independence we need to store
So in theory we would need to store:
In practice we need to store:
Part c
Yes. If A is the cause and each