FIFO Queues

FIFO: First In First Out
sort of like waiting in line at a restaraunt
2 implementations of this:
- Single Linked Lists
- Arrays

Heres a visualization

both implementations are essentially the same, just keeping track of the first and last nodes / idxs and updating their positions
imo its easier with a single linked list

HashTables

Allows for searching data in constant time
One of the 1st things to think of when trying to solve a search/lookup leetcode esq problem

P a i r s O f K e y => H a s h V a l u e => i n d e x

Collision Resolution

2 items trying to go to the same cell

Solution: Linked lists

Seperate Chaining

M = table size h(k) = k%m

using a number like 10 as a size is a bad idea for hash tables
we tend to use Prime Numbers

Inserting data at beginning is good when new data is searched more frequently

Ratio between M = table size: 10 N = Number of items in table: 6

α = \frac{N}{M} = \frac{6}{10} = .6

α = load factor

When the load factor(α) goes past threshold
- Resize it ! (usually multiply m by 2)
- Good threshold size is .75

Heres a visualization

Resizing Tables

Ans: Double the space

M = 10 => m = 20 -> h(k,20) = k % 20

| 0  |  |
| 1  |  |
| 2  |  |
| 3  |  |
| 4  |  |
| 5  |  |
| 6  |  |
| 7  |  |
| 8  |  |
| 9  |  |
| 10 |  |
| 11 |  |
| 12 |  |
| 13 |  |
| 14 |  |
| 15 |  |
| 16 |  |
| 17 |  |
| 18 |  |
| 19 |  |

Once resized, Rehash all items from original table to new table

TC: θ(N + M)

Have to go through N Linked lists & size of M table

How to initialize without resizing

expected N = 100 & α = 0.7

α = \frac{N}{M} < 0.7 => N < 0.7 * M => M > \frac{N}{0.7} = 142.83 . . .

M >= 143 (You should pick a prime number to be you M)

Hash Functions

Mod = %

h (k, M) = K (m o d) M

M should be a prime number

h (k, M) = f l o o r ((k - a) / (b - a) * M)

simple if random key
A <= k < B

h (k, M) = f l o o r (k * A m o d 1)

0 < A < 1
good A = golden ration = 1.61803399
Good wehn m is not prime, (m = power of 2)

Open Addressing

use empty cells in the table to store colliding elements
M > N
α - ratio of used cells from the table ( < 1)
Probing - examining slots in the table.
Number of probes = number of slots examined.
h(k,f,M) where f gives the number of failed probes/attempts
- f=0,1,2,3... until successful hash

Linear probing

h (k, f, M) = (h 1 (k) + f) (m o d) M

if the slot where the key is hashed is taken, use the next available slot and wrap around the table.
Very bad method:
- This causes Primary Clustering or long chains; creating a snowball effect: the longer the chain, the higher the chance to grow

3 rehash (linear)

h (k, f, M) = (h 1 (k, M) + 3 f) (m o d) M

Bad method: Secondary Clustering
- if two keys hash to the same value they follow the same set of rpobes. But better than linear
(this can be done with a different # multiplied rather than three) (e.g. 9f)

Quadratic Probing

h (k, f, M) = (h 1 (k) + c 1 f + c 2 f 2) (m o d) M

Bad method: Secondary Clustering
- if two keys hash to the same value they follow the same set of rpobes. But better than linear

Double Hashing

h (k, f, M) = (h 1 (k, M) + f * h 2 (k, M)) (m o d) M

h2(k,M) should NEVER be 0 (e.g. use: h2(k,M) = 1 + k %(M-1))
Use a second hash value as the jump size ( as opposed to size 1 in linear probing).
Want: h2(k) relativly prime with M. (Relatively prime = they have no common divisor)
- M prime and h2(k,M) = 1 + k % (M-1)
- M = 2^p and h2(k,M) = odd M and h2(k) will be relatively prime since all the divisors of M are powers of 2, thus even.

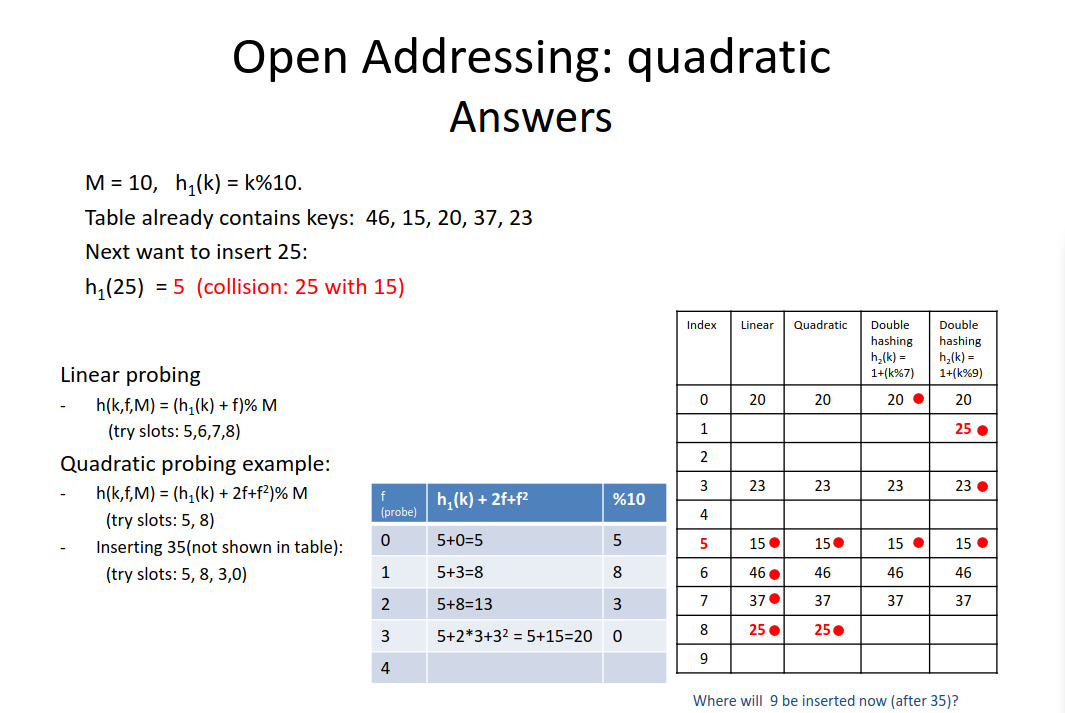
k=25 m=10
h1(25,10) = 25 % 10 = 5
h2(25,10) = 1 + 25 % (10-1) = 8
--------------------------------
h(25,f,10) = (5 + f * 8) % 10
h(25,1,10) = (5 + 1 * 8) % 10 = 3
h(25,2,10) = (5 + 2 * 8) % 10 = 1

worksheet on how each of the addressing methods work

alt text

Two Sum

This is an leetcode side problem

[2,3,5,7,11,15] target = 9

at 5 search for 4 in hashtable if found, found solution!
if not put 5 at idx 2 (5,2) -> (nums[j], j)

start with empty hashtable

idx = idx# => val => search for target-val => found/not => insert/return

idx = 0 => 2 => search for 9-2=7, not found => insert (2,0) in table
idx = 1 => 3 => search for 9-3=6, not found => insert (3,1) in table
idx = 2 => 5 => search for 9-5=4, not found => insert (5,2) in table
idx = 3 => 7 => search for 9-7=2, found => (2,0) return (3,0)

here in the hash table we put pairs of (key, one piece of info) (key,idx)
but there could be different types of cases:
(key, collection) or (key, count)

Search and Deletion in Open Addressing

Searching:

Report as not found whe landing on an empty cell Deletion:
Mark cell as 'DELETED', not as an EMPTY cell
- otherwise you break the chain and not be able to find elements following in that chain.
- E.G. with linear probing, adn hash function (h,i,10) =(k+i)%10, insert 15,25,35,5, search for 5 then delete 25 and search for 5 or 35

idx	linear	operations
0	20	search for 35 => 35 % 10 = 5
1		insert 35 => idx 9
2		delete 25
3	23	search 35 =? idx 5,6,7,8? no
4		cont. =>
5	15*	X = deleted
6	46*	* = visited
7	37*
8	25* X
9	35

When deleting you need to mark that the data was deleted

Expected TC for hash operations

This is under 'perfect' conditions

Operation \ Methods	Separate chaining	Open Addressing
Successful search	Θ(1+α)	(1/α)ln(1/(1-α))
Unsuccessful search	Θ(1+α)	1/(1-α)
Insert	Θ(1) When: insert at beginning and no search for duplicates	1/(1-α)
Delete	Θ(1) Assumes: doubly-linked list and node with item to be deleted is given.	The time complexity does not depend only on α, (but also on the deleted cells). In such cases separate chaining may be preferred to open addressing as its behavior has better guarantees.
Perfect conditions	simple uniform hashing	uniform hashing

FIFO Queues ​

HashTables ​

Collision Resolution ​

Seperate Chaining ​

Resizing Tables ​

Hash Functions ​

Open Addressing ​

Linear probing ​

3 rehash (linear) ​

Quadratic Probing ​

Double Hashing ​

worksheet on how each of the addressing methods work ​

Two Sum ​

Search and Deletion in Open Addressing ​

Expected TC for hash operations ​